Ard Ri in Rust, Part 2: Minmax and Our First Engine

Last time, we implemented the widely unknown tafl game Ard Ri in Rust. Today, we start work on an engine that analyzes Ard Ri positions. We will develop our engine incrementally. Our first goal is a simple minimax engine that evaluates a position and proposes a best move. Future improvements will include

• alpha-beta pruning
• transposition tables
• iterative deepening
• principal variations
• NNUE evaluation

But for now, just the easy thing. We need to implement two components:

• An evaluation function that assigns a numeric score to an Ard Ri position.
• The minimax algorithm for searching through the game tree.

In the wild world of chess programming evaluation functions can get quite complicated. In practice, most chess engines use a NNUE. We’ll get to that, but it turns out you can get pretty far with a braindead evaluation function.

A braindead evaluation function

Recall that in Ard Ri, the defender wins if their king reaches a corner square. The attacker wins if they capture the king. So I propose the following evaluation function:

(# attackers) + (# attackers adjacent to king) - (# defenders + 1 [king]) + (king distance to nearest corner)

Since the starting position for Ard Ri looks like this:

7 # . V V V . # 
6 . . . V . . . 
5 V . O O O . V 
4 V V O K O V V 
3 V . O O O . V 
2 . . . V . . . 
1 # . V V V . # 
  a b c d e f g 

the starting position evaluates to 16 + 0 - 9 + 6 = 13. That’s a weird number, but that doesn’t matter for now. We can worry later about normalizing it. (Chess engines, for example, try to normalize so that a pawn in an endgame is worth roughly 1 point.)

We create a file eval.rs and start it like this:

// eval.rs
use crate::board::{inbounds, rc_to_index, Bitboard, Board, BOARD_SIZE, DIRS};

fn total_board(b: Bitboard) -> i16 {
    return b.count_ones() as i16;
}

The total_board function tells us how many pieces are on a bitboard. (Side note: the count_ones method is from the Rust standard library. In general, computing the number of nonzero bits is the Hamming weight problem. As far as I can tell, Rust simply punts to LLVM for its implementation. Some processors, including modern x86 processors, have hardware optimizations for this computation.)

Computing the king distance to the nearest corner is also easy.

// eval.rs
fn dist_to_corner(b: &Board) -> i16 {
    let (mut king_row, mut king_col) = b.king_coordinates();

    if king_row > BOARD_SIZE / 2 {
        king_row = BOARD_SIZE - king_row;
    }
    if king_col > BOARD_SIZE / 2 {
        king_col = BOARD_SIZE - king_col;
    }

    return (king_row + king_col) as i16;
}

Getting the number of attackers is slightly annoying because we have to convert between bit indices and coordinates, but it’s not so bad.

// eval.rs
fn attackers_next_to_king(b: &Board) -> i16 {
    let mut s = 0;
    let (king_row, king_col) = b.king_coordinates();
    for &(dr, dc) in DIRS.iter() {
        let new_row = king_row as isize + dr;
        let new_col = king_col as isize + dc;
        if !inbounds(new_row, new_col) {
            continue;
        }
        let new_index = rc_to_index(new_row as u64, new_col as u64);
        if b.attacker_board & (1 << new_index) != 0 {
            s += 1;
        }
    }
    return s;
}

Now we can evaluate:

// eval.rs
pub fn naive_eval(b: &Board) -> i16 {
    if b.attacker_win {
        return 10000;
    }
    if b.defender_win {
        return -10000;
    }

    let attacker_weight = 1;
    let defender_weight = 1;
    let mut attack_score = total_board(b.attacker_board);
    let mut defender_score = total_board(b.defender_board) + total_board(b.king_board);

    let attackers_next_to_king = attackers_next_to_king(b);
    let dist_to_corner = dist_to_corner(b);
    defender_score -= dist_to_corner;
    attack_score += attackers_next_to_king;

    return attacker_weight * attack_score - defender_weight * defender_score;
}

We might want to assign global constants to the winning scores of 10000 and -10000, but we can worry about that later.

minimax

The minimax algorithm is the secret sauce that elevates our braindead evaluation function into something that might actually be good. The idea is to traverse the game tree depth first; if we reach a terminal node (or hit a specified depth limit), we return the evaluation of that node.

If it’s the maximizing player’s turn (the attacker, in our game), we recursively compute the minimax value at each possible next move. The best move is the one with the maximum value.

If it’s the minimizing player’s turn (the defender), we do the same, except we pick the move with the minimum score.

In other words, we assume at each node that the opponent will pick the move that optimizes their own score, and we choose our move accordingly.

For example, suppose the game tree looks something like this.

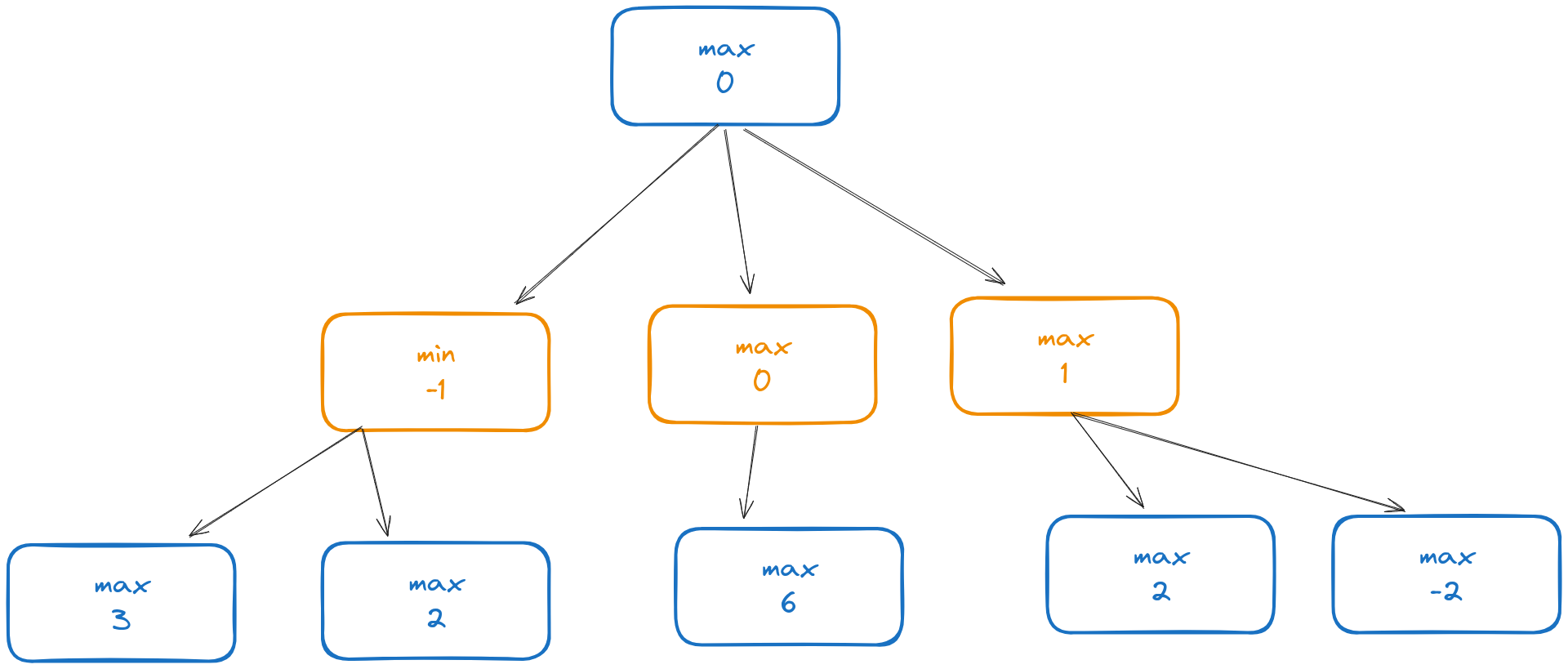
Here a node is colored blue if it’s the maximizing player’s move and orange if it’s minimizing player’s move. The number at the node represents the result of evaluating that position. Minimax descends depth-first through this tree, visiting the max 3 and max 2 nodes at the lower left. Since these are terminal nodes, their evaluations are just 3 and 2, respectively.

Because the minimizing player gets to pick which of those nodes they go to, if we at any point reach the min -1 position on the middle left, we know we will go to the max 2 position because that’s the minimal evaluation from there.

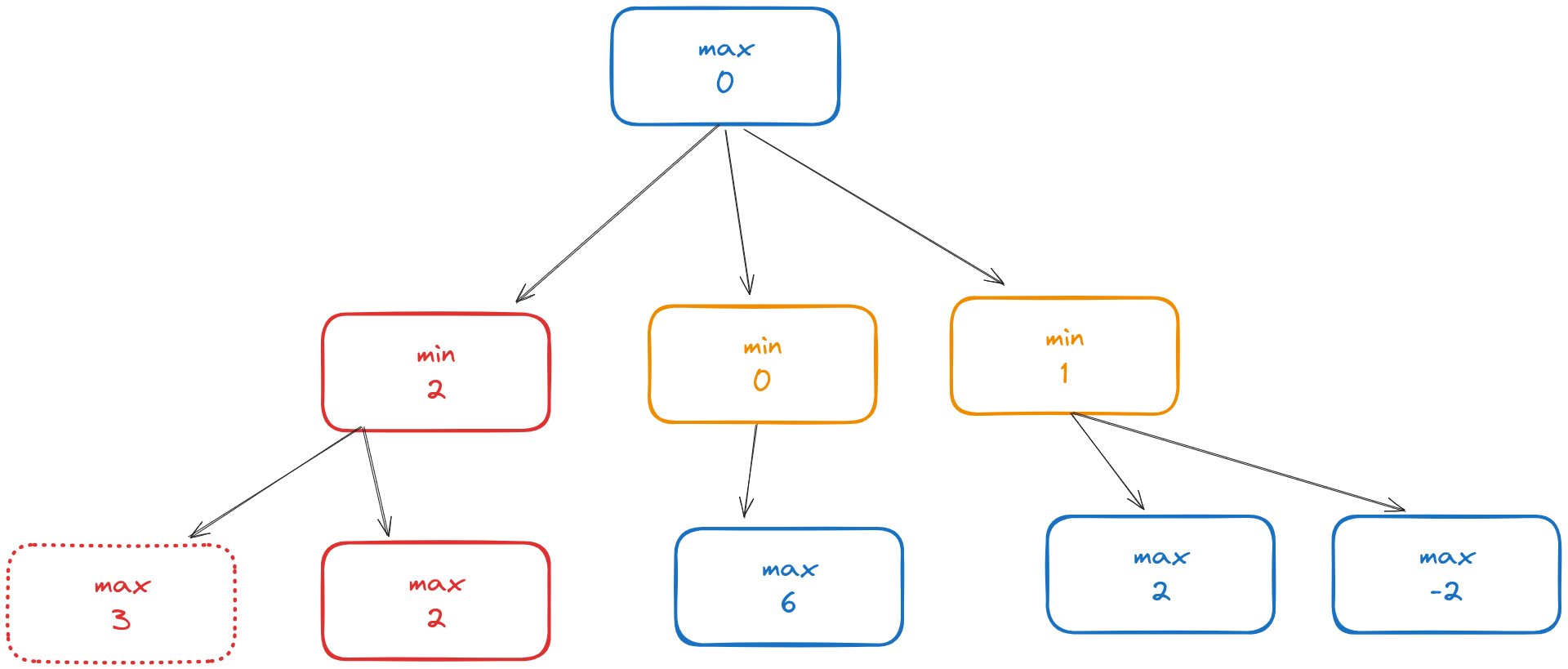
The minimax algorithm then labels that left middle node with 2: that’s the new evaluation of that position. We then descend the middle branch:

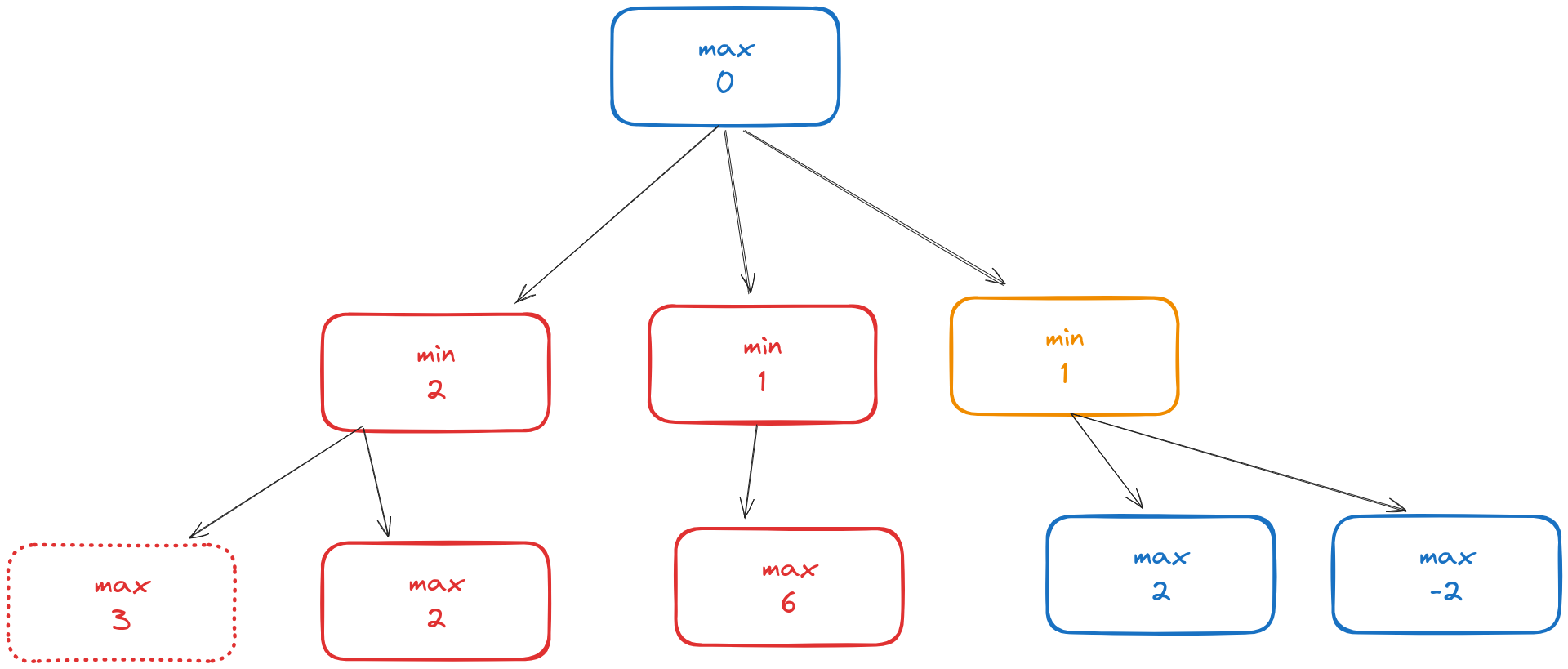
And then the right branch:

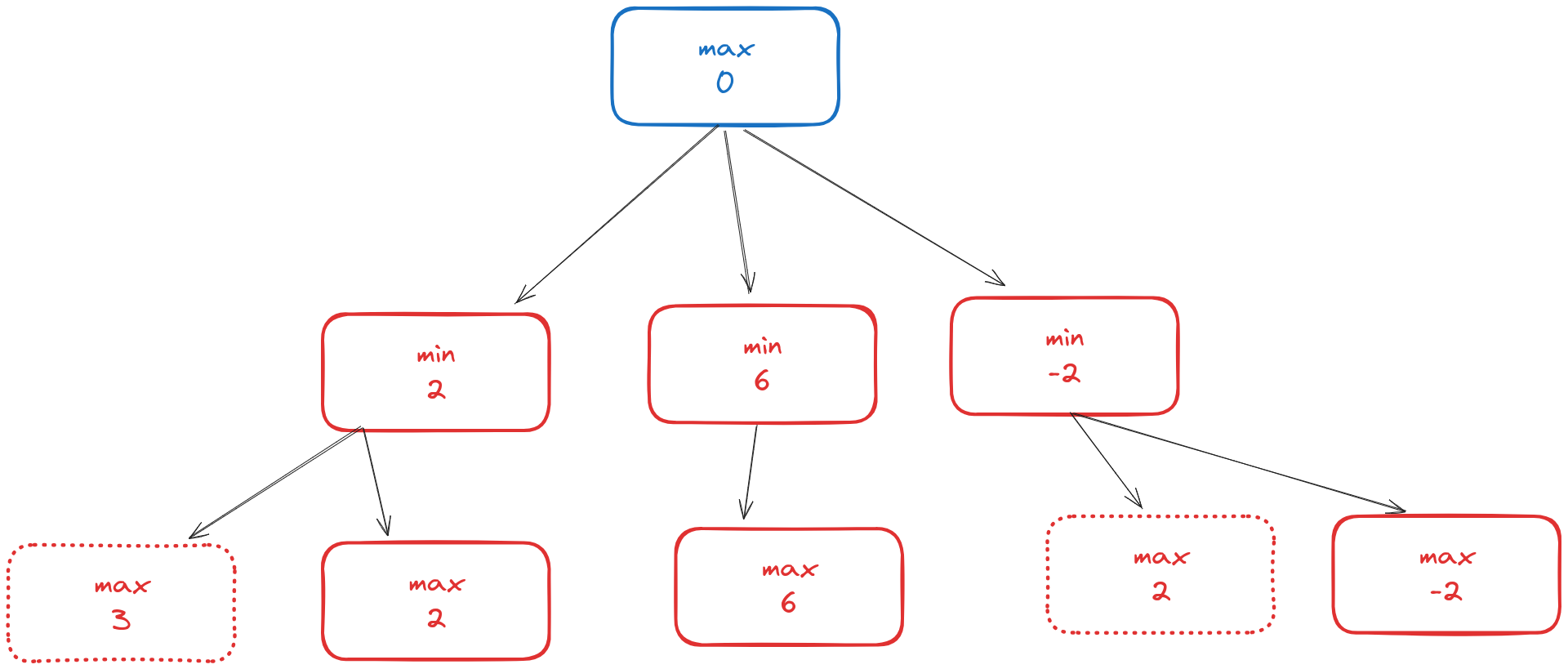
Since the blue node at the top is for the maximizing player, they select the move with the maximal value, which is the middle node:

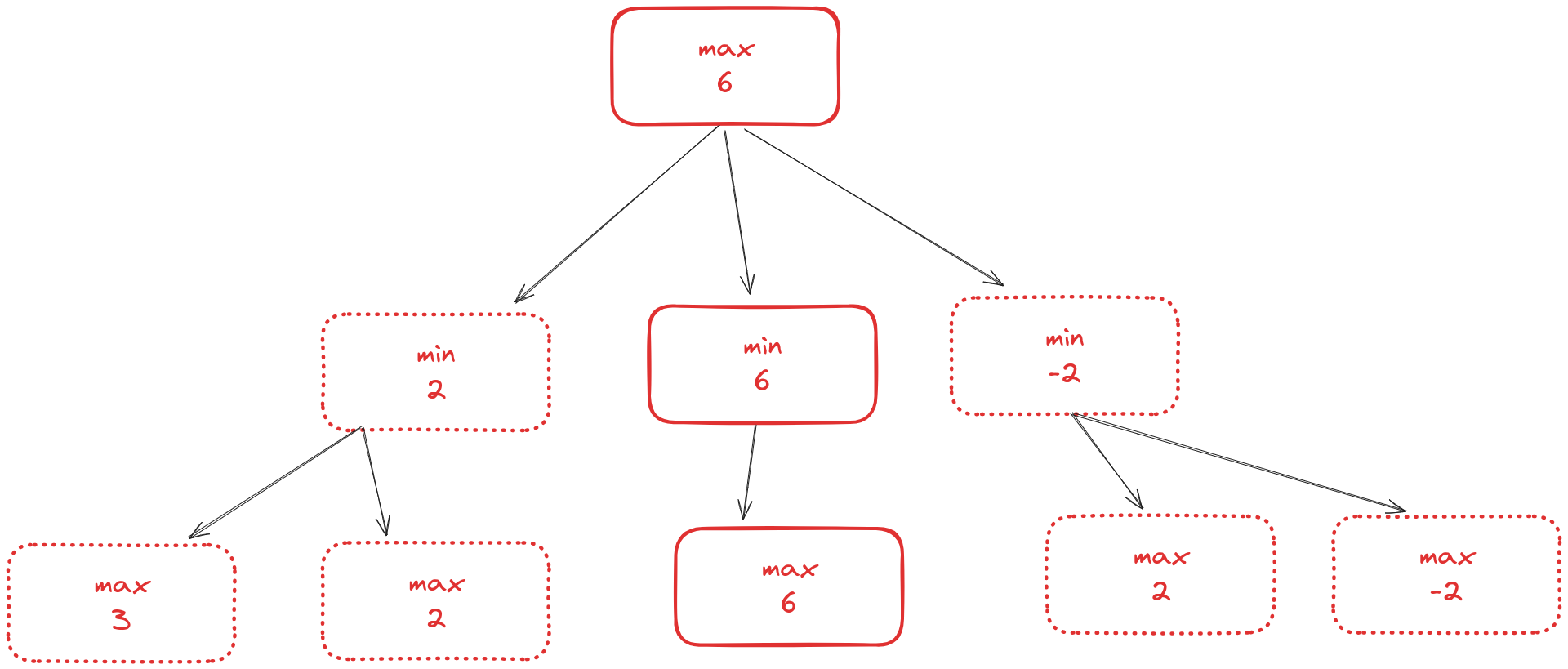
minimax in Rust

To code this in Rust, we create a new file engine.rs

// engine.rs
use crate::board::{Board, Move};
use crate::eval::naive_eval;
use crate::movegen::MoveGenerator;

pub struct TaflAI {
    pub max_depth: u8,
}

We’ll add more parameters to the TaflAI type eventually (things like max nodes, timeout, etc.). We might as well add an EngineRecommendation type to wrap up the engine output.

// engine.rs
pub struct EngineRecommendation {
    pub evaluation: i16,
    pub best_move: Move,
    pub nnodes: usize,
}

The fields are as follows:

• evaluation is the minimax evaluation of the best move
• best_move is the corresponding move
• nnodes is the number of nodes visited by the algorithm

To code minimax, we’ll use a recursive function with signature

fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {}

It will update the nnodes field every time it hits a node. We’ll first call it with depth=TaflAI.max_depth and then subtract one each time we go deeper in the tree. That means if we hit depth 0, then we’re done and can simply return the evaluation of the position.

// engine.rs
fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {
    *nnodes += 1;
    if depth == 0 {
        return EngineRecommendation {
            evaluation: naive_eval(&b),
            best_move: ???, // oh no!
            nnodes: *nnodes,
        };
    }
// ...
}

Ok, one thing we didn’t think about is how to recurse properly through our EngineRecommendation type. This type ostensibly tracks the best move at each node, but when it hits the final depth, we don’t have any more moves to look at! There’s a sketchy but flexible way around this. In board.rs we add a NULL_MOVE constant

// board.rs
pub const NULL_MOVE: Move = Move {
    start_row: 0,
    start_col: 0,
    end_row: 0,
    end_col: 0,
    king_move: false,
};

This is a Move in the literal sense, but may not be a valid move. However, if we never use 0 as the max depth for our AI, it will never actually recommend the NULL_MOVE, so it’s “safe” to do this:

// engine.rs
use crate::board::{Board, Move, NULL_MOVE};

fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {
    *nnodes += 1;
    if depth == 0 {
        return EngineRecommendation {
            evaluation: naive_eval(&b),
            best_move: NULL_MOVE,
            nnodes: *nnodes,
        };
    }
// ...
}

The next thing we’ll add is easy evaluations for victories. We’ll also adjust victory scores by the number of moves required for victory so that victory in 4 moves is better than victory in 5 moves, and so on.

// engine.rs
fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {
    // ...
    if b.attacker_win {
        return EngineRecommendation {
            evaluation: 10000 + depth as i16,
            best_move: NULL_MOVE,
            nnodes: *nnodes,
        };
    }

    if b.defender_win {
        return EngineRecommendation {
            evaluation: -10000 - depth as i16,
            best_move: NULL_MOVE,
            nnodes: *nnodes,
        };
    }
    // ...
}

Now we get to the heart of the matter. Suppose first it’s the attacker’s move. Then we iterate through all possible moves and pick the one whose minimax score is the highest.

// engine.rs
fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {
    //...
    if max_player {
        let mut max_eval = i16::MIN;
        let mut best_move = NULL_MOVE;

        // iterate through all possible moves
        for m in MoveGenerator::new(&b) {
            let new_board = b.make_move(m);
            let eval = minimax(&new_board, depth - 1, false, nnodes);

            // update with the best move
            if eval.evaluation > max_eval {
                max_eval = eval.evaluation;
                best_move = m;
            }
        }
        return EngineRecommendation {
            evaluation: max_eval,
            best_move: best_move,
            nnodes: *nnodes,
        };
    }
    // ...
}

There’s a weird edge case here when there are no legal moves. We’ll handle that eventually. In fact, that requires an update to our rule book. Some sources say the attacker wins in this case, some say it’s stalemate. Edge cases notwithstanding, we have almost the identical code for the minimizing player:

// engine.rs
fn minimax(b: &Board, depth: u8, max_player: bool, nnodes: &mut usize) -> EngineRecommendation {
    //...
    if max_player {
        // ...
    } else {
        let mut min_eval = i16::MAX;
        let mut best_move = NULL_MOVE;

        for m in MoveGenerator::new(&b) {
            let new_board = b.make_move(m);
            let eval = minimax(&new_board, depth - 1, true, nnodes);
            if eval.evaluation < min_eval {
                min_eval = eval.evaluation;
                best_move = m;
            }
            min_eval = min_eval.min(eval.evaluation);
        }
        return EngineRecommendation {
            evaluation: min_eval,
            best_move: best_move,
            nnodes: *nnodes,
        };
    }
}

Now we add a public-facing method to TaflAI that executes minimax:

// engine.rs
impl TaflAI {
    pub fn find_best_move(&mut self, b: &Board) -> EngineRecommendation {
        let mut nnodes = 0usize;
        return minimax(b, self.max_depth, b.attacker_move, &mut nnodes);
    }
}

Making it run

For benchmarking purposes, I want not only to count the nodes we see (which we’re already doing), I also want to measure the time the evaluation takes. Decreasing the number of nodes visited and the time it takes to process a node are the two primary avenues for performance gains.

To this end, we add one more type to our engine.

// engine.rs
pub struct EngineBenchmark {
    pub recommendation: EngineRecommendation,
    pub elapsed: std::time::Duration,
}

and we update the UI to handle engine output

// ui.rs
pub trait UI {
    fn get_move(&mut self) -> Move;
    fn render_board(&self, b: &Board);
    fn render_eval(&self, benchmark: &EngineBenchmark);
    fn invalid_move(&self);
    fn attacker_win(&self);
    fn defender_win(&self);
}

All that remains is to update our main game loop.

// main.rs
use std::time::Instant;

use movegen::MoveGenerator;
use ui::UI;

mod board;
mod engine;
mod eval;
mod movegen;
mod ui;

// ...
fn main() {
    let mut b = init_board();
    let mut tafl_ai = engine::TaflAI { max_depth: 6 };
    let mut console_ui = ui::ConsoleUI::new();

    loop {
        if b.defender_win {
            console_ui.defender_win();
            break;
        } else if b.attacker_win {
            console_ui.attacker_win();
            break;
        }

        console_ui.render_board(&b);
        let now = Instant::now();
        let recommendation = tafl_ai.find_best_move(&b);
        let elapsed = now.elapsed();
        let benchmark = engine::EngineBenchmark {
            recommendation,
            elapsed,
        };
        console_ui.render_eval(&benchmark);

        let mut mv = console_ui.get_move();

        let legal_moves = MoveGenerator::new(&b).collect::<Vec<_>>();
        while !legal_moves.contains(&mv) {
            console_ui.invalid_move();
            mv = console_ui.get_move();
        }
        b = b.make_move(mv);
    }
}

Running it now looks like this:

7 # . V V V . # 
6 . . . V . . . 
5 V . O O O . V 
4 V V O K O V V 
3 V . O O O . V 
2 . . . V . . . 
1 # . V V V . # 
  a b c d e f g 

Recommended Move: c3c2
Evaluation: 13 (10328649 nodes) (7.20s)
Make a move: 

If I make the recommended move c3c2, I get this:

7 # . V V V . # 
6 . . . V . . . 
5 V . O O O . V 
4 V V O K O V V 
3 V . . O O . V 
2 . . O V . . . 
1 # . V V V . # 
  a b c d e f g 

Recommended Move: e1e2
Evaluation: 13 (16555100 nodes) (10.06s)

Wrap up

Minimax is slow! Even at depth 6 it takes about 10 seconds to evaluate a position. To be fair, it’s processing 16,555,100 nodes, so 1,655,510 nodes per second, but still, that’s a lot of processing time for very little reward. Our next step in this journey is to reduce the number of positions that the engine has to actually look at, which we will do through a combination of techniques.

Spoiler! After we implement alpha-beta pruning, that first position will require only 47 milliseconds to evaluate at depth 6, and it will cover approximately 71,00 nodes. The second position will require only 43ms and will see about 46,000 nodes.